Polinom
İndisler ile numaralayacağımız bir dizi sonlu, gerçek değer seçelim. Meselâ şunları alalım;
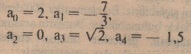
Bunları indislere eşit üstelli bir değişkenle çarpalım., ve hepsini toplayalım, elde edilen sonuç
![]()
Bu ifade genelleştirildiğinde x değişkenli bir polinom fonksiyonu elde edilir,
![]()
Bu ifadede x değişkeni, y veya+z ile değiştirildiğinde veya sinx, logx tipindeki fonksiyonlarda P(x) fonksiyonu değişerek P(y), P(z), P(sinx) vs. haline dönüşür. Ancak fonksiyonun yapısında genel anlamda değişiklik olmaz, a,), a,, a2, a3, a4katsayılan değişmeden kalır. Bu yapı polinom adını alır. Genellikle gerçek kat sayılı n’inçi dereceden polinomlardan söz edilir, n1. dereceden bütün kat sayıların 0 olduğu durumda, a„’de 0 olur.
Konuşma lisanı kötüye kullanılarak “P” polinomu ile “P(x)” polinom fonksiyonu genellik¬le birbirine karıştırılır. Polinom bir terimliyse (3×4) monom, iki terimliyse (3-x) binom, üç terimliyse trinom adım alacaktır.
İki polinomun toplanmasında, aynı indisli katsayıların sırayla toplanması yapılır;
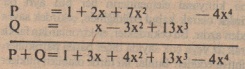
Çarpma işlemi ise, iki toplamın çarpımına benzer olarak gerçekleştirilir. Mesela;
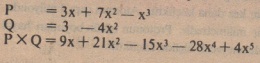
Çarpımın derecesi; her çarpan polinomun dereceleri toplamına eşittir.
![]()
Bir k sabitiyle bir polinomun çarpımında
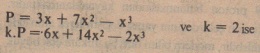
- Toplama ve çarpmaya göre polinom kümesi değişmeli bir birim halka yapısı kazanır.
Toplama ve bir sabit ile çarpımına göre R üzerinde vektörel düzlem yapısı gösterir.
Polinom n veya n’den küçük dereceli ise; bu düzlem n+l’e eşit boyutludur. Bu düzlemin bir tabanını belirlemek için; 1,x,x2,x3…x” monomlarından yararlanılır.
İki değişkenli polinomlarda tanımlanabilir: Mesela P.(x,y)=xy+3xy2-4x3y3 veya 3, 4, , n değişkenli polinomlarda tanımlanabilir.
- İki değişkenli polinomların yazımında 2 indisli katsayılar kullanılır. Birinci indis ilk değişkenin derecesini, ikinci indis ikinci değişkenin derecesini belirtir. Örneğimizde aı,ı=l, aı,2=3, a3,3=-4’tür. Diğer p o’dır. n değişkenli bir polinomda, n indisli katsayılara gereksinim vardır.


Yorumlar
Henüz yorum yapılmamış.