• Günlük hayatımızda şu cümlelerin sık sık tekrarlandığım biliriz: “Bu sınavda başarılı olma şansı çok yüksek”, “Atılan bir bozuk parada yazı elde edilme şansı ikide birdir”, “Bir tekpiyango bileti ile kazanma şansı çok düşüktür”. Çıkar yolu belli olmayan her türlü olayda, oluşacaktan yaklaşıklıkla önceden belirlemeye çalışırız. Olasılıklar teorisi de bu tür açıklamalara matematiksel bir ifade kazandırır ve oluşabileceklerin hesabını gerçekleştirir.

• Bir kaç örnekle bu tür olasılıklan daha iyi analiz edebiliriz: Üç adayın karşı karşıya olduğu bir seçimde Dubois‘in kazanma şansı 1/6, Dupont‘un 1/2, Durand’ın ise 1/3‘dür. Dupont veya Durand‘ın kazanacağı, yani Dubois’in kazanamayacağı olasılık belirlenebilir. Bu olasılık 5/6 (1/2+1/3)‘dır. Aynı şekilde Dubois veya Dupont’un kazanan olduğu durumun olasılığı 2/3‘dür. Dubois ve Dupont’un beraberce kazanma olasılıkları dır. (imkansız olay).

• Bir bozuk para üç defa ard arda atıldığında, iki defa yazı gelme olasılığı nedir? İlk bakışta dört olası cevap varmış gibi gözükür; 0,1,2 veya 3 yazı gelmesi. Bu dördünün yher birinin olasılığı 1/4‘dür. Sonuçta 8 olası çözüm olacağı görülür. Bunlar YYY, YYT, YTY, YTT, TYY, TYT, TTY, TTT. Bu sekiz sonuçtan herbiri eşit olarak olasıdır, bunların arasında ilci defa üstüste yazı gelen üç tanedir. O halde iki defa yazı elde edilme şartı 3/8‘dir.

• Bir öğrencinin ingilizce sınavını başarma olasılığı %40, tarih sınavını %30, bu iki sınavı da başarma olasılığı %10‘dur. Bu sınavlardan en azından birinde başanlı olma olasılığını belirlemek için sınavlardan herbirini başarma olasılıklarını toplamak gerekir. Ancak o zaman her iki sınavı da başarma olasılığı olan % 10 iki defa hesaplanmış olur. O halde bu %10 toplamdan çıkarılmalıdır. Bu iki sınavdan en azından birinde başarılı olma olasılığı P=%40+%30-%10=%60 eşitliği ile hesaplanır.

• Bir silah atıcısı atışlarının %80‘inde başarılıdır. Aynı şartlardaki ikinci bir atıcı ise atışlarının %70’inde başarılıdır. İki atıcının aynı anda silah çekmeleri durumunda hedefin vurulma olasılığı nedir? Birinci atıcı; attığı her 100 atışta 80 kere hedefi vurur. Kalan 20 atışta ise, ikinci atışta 14 kez (10 da 7) başarılı olabilir. Bu şekilde 100 atışın 94’ünde hedefin vurulduğu söylenebilir. Hedefin atıcılardan en azından biri tarafından vurulma ihtimali %94‘dür.

• Bu durumun matematik olarak ifade edilmesi de mümkündür.

• U elemanlı bir küme ele alalım. Bir olay da Unun X alt kümesini oluştursun. U kümesi üzerinde bir olasılık kuramının belirlenmesi, aşağıdaki kurallara uyarak u kümesinin her alt kümesine bir sayı tekabül ettirilmekle gerçekleştirilir.

• Her X alt kümesi için, X’e tekabül eden sayıda P(x) o arasında olmalıdır.
  o < rXX) <ı
• U’ya tekabül eden sayı 1’dir; p(U) = 1 ;p(0) = O

• îki X ve Y olayı için, X U Y(X veya Y)olayı ve X Y(X ve Y) olayı gözönüne alınabilir. Bu durumda şu eşitlik gerçeklenir:p (X U Y) =rxx) + p(Y) – p(X n Y).

– Bu kurallann iki sonucu vardır:
1. X’ X’in ters olayını belirliyorsa, yani yalnız ve yalnız X’in gerçekleşmediği durumda gerçekle-şense;p (X’) = 1 – p (X)tir.

X’ U içindeki X’in tümleyen alt kümesidir.

2. X ve Y aynı anda gerçekleşemeyecek olaylarsa; ,(X n Y = 0 ),’dir.
Bu durumda üçüncü kural şu şekle dönüşür: p (X U Y) = p (X) + p (Y).

n adet eşit olarak olası ve zıt elementer olaydan oluşmuşsa, bunlardan herbirinin olasılığı l/n olarak belirlenir. Tamamiyle dengeli kabul edilen 6 yüzlü bir zar atıldığında, istenen bir yüze düşme olasılığı 1/6’dır.

• Üzerinde bir ihtimaliyet belirlediğimizi kabul edelim. X olayının iyi belirlenmiş bir P(X) olasılığı olur. Şimdi de ayn bir bilgiyi ekleyelim; bu bilgi Y olayının da gerçekleşmiş olduğudur. Bu bilgi X olayının olasılığını değiştirir. Bu yeni olasılık veya X’in koşullu olasılığı P'(X) ile ifade edilir. X’in gerçekleşmesi için XUY’nin gerçekleşmiş olması gerekir. P'(X)in belirlenmesi Y kümesine göre XUY’nin belirlenmesi demektir.

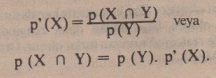
• X ve Y olayının beraber gerçekleşme olasılığı bunlardan birinin olasılığı ile, birinci oluştuğunda diğerinin koşullu olasılığının çarpımına eşittir.

• Olasılıkta bağımsız olaylar şu şekilde gelişir: X ve Y olaylarının bağımsız olması için, birinin gerçekleşmesi, diğerinin olasılığını değiştirmemesi gerekir, yani P(X)=P'(X) olmalıdır.

• Bu teorinin uzatılması da mümkündür. Olay bir veya birçok sayıyla karakterize edildiğinde, bir veya birçok boyutlu tesadüfi değişken kavramı ortaya çıkar. En bilinen ve en sıklıkla kullanılan kanunlar binomiyal, normal veya La Place Gauss, Poisson vs. yöntemleridir. Bunlar çok sayıda fenomenin geçerli şekilde belirlenmek-rini sağlarlar. Bunlar belirli şekilli eğrilerdir (Poisson dağılımında çan şeklindedir) ve değişke-nin en olası değerinde bir maksimuma ulaşırlar.

• Olasılık hesaplan Pascal ve Mere ile kumar oyunlan şeklinde ortaya çıkmıştır. Daha sonralan ise matematik, fizik körpüsküler, ekonomi, genetik, psikoloji, yönetim ve seçim problemlerine uzanan bütün bilim alanlarına yayılmıştır. Olasılık hesaplamalarının gerçekleşmesinde enformatiğe başvurulur.