• Çarpmaları basit toplamalara dönüştürebilmek veya bölmeler yerine çıkarmalar uygulayabilmek mümkün müdür? Logaritma bilimi bu sorulara olumlu cevaplar sağlar. Logaritma cetvelleri imtihanlarda öğrencilerin yanında bulunduğundan beri çarpma ve bölmeler, çıkarma ve toplamalara dönüştürülebilmektedir.

• 10’un katlarım yazarak işe başlayalım, ama önce aşağıdaki tablodaki üstel değerlerin logaritmalarını bilelim.

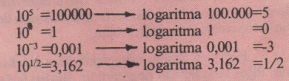
• Bu şekilde sonsuza kadar devam etmek mümkündür. Burada prensip oldukça basittir. Herhangi bir x gerçel sayısı verildiğinde, 10* gerçel pozitif bir sayıdır. Bunun tersi olarak bütün y pozitif gerçel sayılan 10’un üsteli olarak yazılabilir; 10v.y=10v ise, y‘nin logaritması x’dir denir ve x=log y yazdır.

• Logaritma ifadesinin avantajı, matematikte 2 özellik ile çeşitli hesaplamaların kısaltmaları gerçekleştirilir;

1° log a.b=loga+log b

2° log a*=Mog a

• 10 sayısı için gerçekleştirdiğimiz bu işlemler, herhangi bir pozitif gerçel sayı içinde geçerlidir. Pozitif gerçel bir a sayısı seçtiğimizde, her x gerçel sayısına, başka bir y gerçel sayısını tekabül ettirebiliriz. y=a* y sayısı x’in a tabanına göre eksponansiyeli olarak adlandırılır. Tanımla­nan fonksiyon ise a tabanlı eksponansiyel fonksiyondur, a* sayısının her zaman pozitif olduğu unutulmamalıdır.
• Değişik tabanlı logaritmalar arasında, aşağıdaki formülle belirlenen basit bir bağıntı vardır;

logfcy=log6a x İog„y

Bu formülden ise aşağıdaki ifade elde edilebilir, İ0g,/ay= log|/aa. logay= — logay.

• e sayısının logaritmada önemli bir rolü vardır, e sayısı neperyen logaritmanın tabanıdır. Neperyen adı; 1614 yılında bu hesaplamaları ilk defa gerçekleştiren Napier’den kaynaklanmakta­dır, e sayısı rasyonel bir sayı değildir, ondalık sayı olarak yazılışı sonsuza kadar uzar.

e=2,718281828459

e sayısı önemli bir sabittir, matematikte olduğu kadar, fizikte de birçok formülde ortaya çıkar.

• Neperyen logaritmalar Log ile ifade edilir. Logjx fonksiyonunun türevi l/x’tir. Neper­yen logaritma ile ondalık (on tabanfi) logaritma oranı M sabitine eşittir.

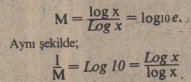
•  Logaritma ve eksponansiyellerin yaklaşık kullanım alanları vardır. Eksponansiyel fonksi­yonlar çeşitli matematik, istatistik, fizik, bioloji, ekonomi vs. formüllerinde karşımıza çıkabilir. Ayrıca eksponansiyel fonksiyon Laplace Gauss yöntemi adı verilen istatistik dağılım kuralının cebirsel ifadesinde de kullanılır. Ekonomi de, sabitartan faiz oranlarında eksponansiyel fonksiyon­dan yararlanılır, t süreside, i faiz oranı uygulanan C ana parası C(l+i) şekline dönüşür.

• Sayısal hesaplamalarda, ondalık logarit­maların kullanımı hesaplan kolaylaştırır, loga^fc=b log a formülü ile bir üstel hesabı çarpmaya dönüştürülebilir. Bu tür hesaplamalarda logarit­ma cetvellerinden yararlanılır.

• Hesap kuralları, bu hesaplama prensiple­rine dayalıdır. İki çubuğun veya doğru parçasının uçuça konması uzunluklarının hesaplanmasına yarar; bu uzunluklar sayıların logaritmalarını gösterir.lO ve 100 arası, 1 ve 10 arasının aynıdır. Yani iki sayının çarpımı yerine, bu sayıların logaritmalarının toplamı yazılabilir. Örneğin 2’yi 3 ile çarpmak yerine, birinci cetvelin Tinin karşısına ikinci cetvelin 2’si getirilir ve sonuç; birinci cetveldeki 3’ün karşılığının ikinci cetvelden okunması ile bulunur.