• Birçok haklı sebeplerden dolayı Fizik ve mekanikte bir değişkenli fonksiyonlar ve bunların birinci, ikinci vs. türevleri kullanılmaktadır. Mesela t’nin fonksiyonundaki bir x uzaklığının, hızı x'(t), ivmesi x”(t) türevleri ile hesaplanır. Kendisine sorulan probleme göre bir fizikçi bu değişik fonksiyonları birleştirerek bir diferansiyel denklem haline dönüştürür.

• Birinci dereceden bir diferansiyel denklem bir değişken, bir fonksiyon ve bu fonksiyonun türevini ihtiva eder. O halde;

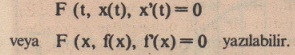
Bu denklemin ikinci dereceden olabilmesi için türevi bulunması gerekir. Aynı şekilde üçüncü dereceden veya n’ninci dereceden olabilir.

Bir fizikçi bu denklemi yazdıktan sonra, görevi matematikçiler üstlenir ve bu eşitliğin integralini alırlar, yani çözüm olan bir veya birçok f (x) fonksiyonu bulurlar.

Ox ekseninde hareketli bir cisim düşüne­lim. t=0 anında Vo hızı ile x=0’dan geçsin. Ve hızının zamanla arttığuıı varsayalım. V=Vo+kt hareket denklemi V=x(t) yazılarak elde edilir ve eşitlik;

x'(t)=Vo+kt haline dönüşür, tntegrasyon basittir ve

Ancak diferansiyel bir denklemin integralinın alınması her zaman bu kadar basit değildir. Bu amaçla; bu eşitlikleri gruplayıp, her grubun ayrı çözümü geliştirilmiştir. Aşağıda; integral alma metotları araştırılmadan çözülebilecek bazı basit diferansiyel denklemler verilmiştir. Genel anlam­da; bir diferansiyel denklemin integrali alındığında her biri bir veya birçok parametre ihtiva eden sayısız çözüm fonksiyonları elde edilir. Bazı eşitlik gruplanmalan: