Bir eşitliğin derecesi, terimlerinden birindeki bilinmeyenlerin en fazla üstellerinin toplamına eşittir.

x+y=1 eşitliği iki bilinmeyenli, birinci dereceden bjr eşitliktir.
x.y=225 eşitliği iki bilinmeyenli, ikinci dereceden bir eşitliktir

Bilinmeyen x ile belirtildiğinde; ikinci dereceden bir denklemin genel gösterilişi

ax2+bx+c=0 şeklindedir.
a,b,c, reel veya sanal olabilen kat sayılardır.

Bu tür bir eşitliğin çözümünde denklemin kökleri diye adlandırılan ve denklemi doğrulayan x değerlerinin belirlenmesi gerekir. Bu amaçla diskriminant hesaplanır.
▲ =b²-4 ac (a,b,c, belirli kat sayılardır)

▲ değeri köklerin var olup olmadığının anlaşılmasında, eğer kökler var ise de bu köklerin hesaplanmasına yarar.
▲=0 ise denklemin birbirine eşit iki gerçel kökü vardır.

Bu kökler ;

▲ sıfırdan büyük ise, eşitliğin 2 farklı gerçel kökü vardır.

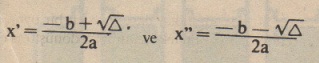
▲ sıfırdan küçükse, yalnız reel (gerçel) sayılarla çalışıldığında negatif sayıların kareköklerinin alınamayacağından bu eşitliğin kökleri yoktur denir. Ancak sanal (kompleks) sayılar kümesinde (C) gerçel köklerin elde yöntemlerine benzer yöntemlerle iki kök elde edilir. A ‘nın eksi işareti yerine 1² yazılır ve karekök alınır.

• İkinci dereceden eşitlikler teknolojinin çeşitli birimlerinde de karşımıza çıkar.  Mesela;

• Bir füzenin enerjisi şu bağıntı ile belirtilir:

F:=Enerji miktarı

m=füzenin kütlesi

v=füzenin hızı

Düşen bir cismin katettiği yol için

e=katedilen yol

g=yerçekimi ivmesi

t=yolu katetmek için gerekli zaman.

• Ayrıca bir rezistansta harcanan elektrik gücünde, ışıklı kaynaktan uzaklaşan bir yüzeyin aydınlanmasında, amplifikatörlerde, volum hesabında da 2. dereceden eşitlikler kullanılır.

• İkinci dereceden bir eşitliğin köklerinin bilinmesi, bu eşitliği oluşturan trinomun işaretinin tanınmasına yarar. O vakit ikinci dereceden bir eşitlik, eşitsizlik haline dönüştürülür.